What Micron Is A Coffee Filter

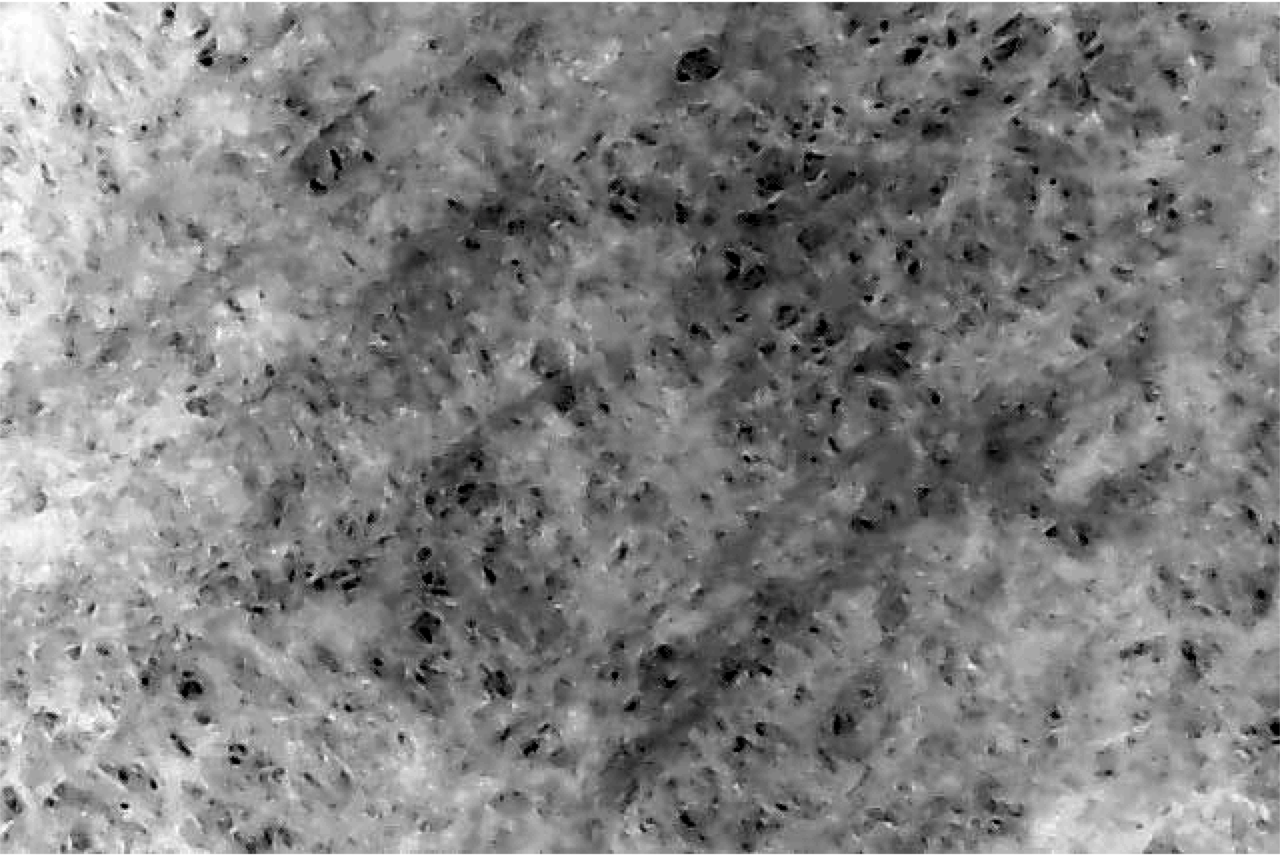
A while agone, I decided to purchase a relatively inexpensive USB microscope to see what V60 filters look like. This is one of the first images I took of a Hario tabbed paper filter:

I was really pleased that the microscope had plenty resolution to see the filter pores ! This opened up the exciting possibility of characterizing the pores of coffee filters, and make up one's mind which ones are optimal for pour over brews. One affair that became immediately apparent is that the pores are not round, and they don't seem produced by a perforation of the paper membrane, instead they simply seem to naturally occur from spacings between piles of paper fibers.

When I saw that nice image, I immediately grabbed a Hario tabless paper filter and took some other paradigm:

Equally you tin see, this one is less immediately interesting, we can barely see the pores ! After being a bit bummed out most this, I realized it was only caused by the tabless filters existence quite thicker, which minimizes the contrast of the microscope's LED light bouncing off the filter surface. Fortunately, it'due south possible to fix this with a bit of image analysis. To do this, I wrote a code that re-adjusts the dissimilarity of the image so that its pores become more than credible:

Past that point, I realized that a proper filter assay was indeed possible with this microscope, and things started to become really fun. I gathered this list of filters from diverse manufacturers:

Hario tabbed V60 bleached newspaper filters [Amazon]
Hario tabless V60 bleached newspaper filters
Hario tabbed V60 unbleached paper filters [Amazon]
Cafec V60 unbleached newspaper filters
"Coffee Sock" V60 cloth filters
Aeropress bleached newspaper filters
Aesir bleached paper filters for Aeropress brewer
Chemex unbleached paper filters
Chemex bleached newspaper filters
Osaka metal filter for pour over
Hario unbleached paper filters for siphon
Hario cloth filters for siphon
Whatman Form 597 quantitative bleached paper filters

Now, before we get-go discussing the actual analysis, I'd like to show you lot what each of them wait like nether the microscope.

Hario Tabbed Bleached Paper Filters for V60

Hario Tabless Bleached Paper Filters for V60

Hario Tabbed Unbleached Paper Filters for V60

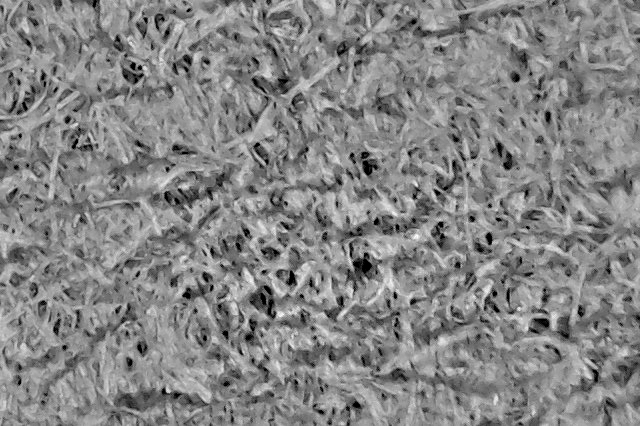
Cafec Bleached Paper Filters for V60

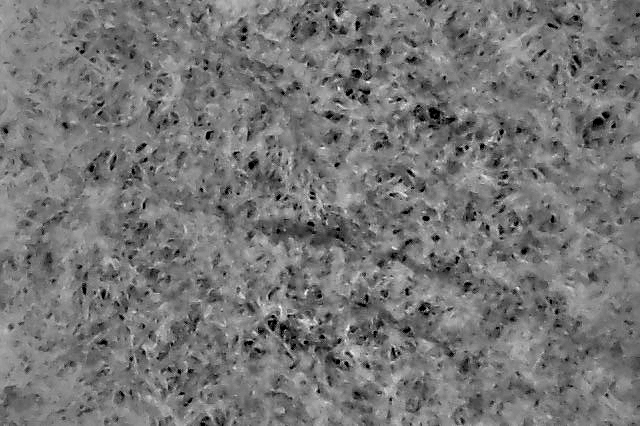
"Coffee Sock" Fabric Filters for V60

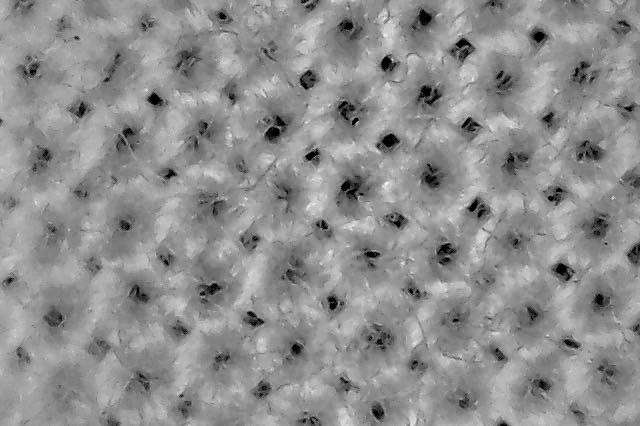
Aeropress Bleached Newspaper Filters

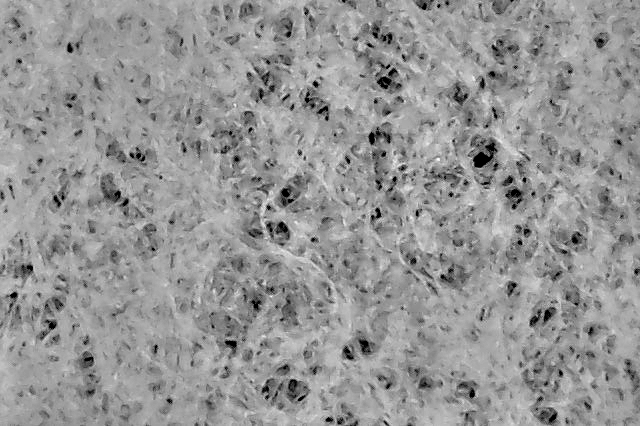
Aesir Bleached Paper Filters

Chemex Unbleached Paper Filters

Chemex Bleached Paper Filters

Osaka Metal Filter for Chemex and V60

Hario Unbleached Paper Filters for Siphon

Hario Cloth Filters for Siphon

Scale of Image Scale

Before these images can be used in a more than quantitative analysis, the size of each pixel must first be determined. To achieve this, the microscope comes with a small scale plastic that looks like this:

Equally you can run into, in that location are many options that can exist chosen from. I highly suspect that the printing standards for this calibration unit are non particularly dandy, and so I decided to choose the grid in the middle of the calibration plastic; I chose it because it provides many measurements of the scale at once, and information technology seems much easier for the manufacturer to become the spacing between printed lines right rather than the thickness of a line. I took seven images of this filigree at slightly dissimilar positions. These images each look like this:

These lines are marked equally 0.1 mm (100 micron) wide. You can already run into from the epitome that the line spacings are non perfectly uniform. In that location are also small defects on the image caused by imperfections in the plastic. I chose to accept the median value of each row (a vertical median) to create a 1-dimensional signal of this grid, which equally y'all can expect looks like an up-and-down pattern (dark pixels where a line falls, white pixels otherwise). I then used what is called an auto-correlation of that signal to determine by how much it can be shifted before lines overlap with each other. I did this on the seven images that I took; I then took the average pixel scale as my all-time measurement, and the standard deviation as the statistical uncertainty in my measurement. This measurement fault does not include any systematics. For case, if the manufacturer actually printed a design of lines averaging 110-micron wide spacing, that x micron systematic error won't be included in my error estimate. Because I have no style to know about such systematics, I just ignored them.

I besides repeated a similar analysis with a vertical median instead of a horizontal ane, to check that the pixel sizes are the same in the vertical and horizontal directions. Here's what I constitute:

Horizontal scale: 67.59 ± 0.09 micron per pixel
Vertical scale: 67.54 ± 0.07 micron per pixel

As y'all tin see, the two values agree within the fault bars, which is encouraging. Therefore I assumed that the scaling is the same in both directions, and combined them together to obtain a last image scale interpretation:

Combined calibration: 67.56 ± 0.08 micron per pixel

Analysis of Pore Distributions

Now information technology's time to get even deeper in the technical details. As I mentioned, i of the more useful things to practise with these microscope images is to determine the uniformity and quantity of pores in each filter. To do this, I opted to do some image smoothing with various bandpass sizes.

The unbleached paper filters I analyzed are chocolate-brown rather than white. Considering I don't want color to bear on my results or brand information technology harder to bring out the contrast between the filter surface and its pores, I experimented visually and adamant that adding upwardly 100% of the red channel and 50% of the green aqueduct was a good way to mitigate the event of brown color on the detection of filter pores. I used none of the blue channel, considering brown is a colour that contains very little blue in it, and this means that the undesirable brown-white variations in color across the surface of an unbleached filter are maximized in the blue channel.

Here's what an original colour image of a Hario unbleached filter looks like:

If we look just at the (contrast-scaled) blue aqueduct, variations in chocolate-brown shade will be very obvious:

If instead we looked at the combined R+G+B channels, these variations would get diluted a bit:

Simply taking the ruddy channel plus half of the green aqueduct gets the states something that removes these variations even more:

As I mentioned before, an of import step is to re-normalize the image contrast in social club to see the pores clearly regardless of filter thickness. In astronomy, I need to do this all the time and by experience i efficient way to do it that is robust against outlier pixels is to subtract the 0.5th percentile of the paradigm everywhere (i.eastward., subtract almost the smallest prototype value), then carve up the image by its 88th percentile (i.e., split up by almost the largest image value). I then set up any outlier pixels darker than zero to exactly null, and whatsoever outlier pixels brighter than 1.0 to exactly 1.0.

Here'southward what the epitome above would look like before applying such a contrast normalization:

The pores are much harder to see in the paradigm above, compared to this one where the contrast was normalized:

There is another neat trick that can be used to remove large-scale variations across the image very efficiently, as long as they are larger in calibration than the largest possible pores. Basically, you split the original paradigm by a smoothed version of itself, and this brings out merely the small-scale variations across the image. I used a Butterworth filter to practice this; it uses a slightly different bandpass to shine the image compared to the more than typical Gaussian smoothing, but I found that it was improve at preserving the exact pore shapes. In all cases I removed simply the x% largest spatial frequencies in all images with this step.

Here's how the Butterworth filtering affects the image above:

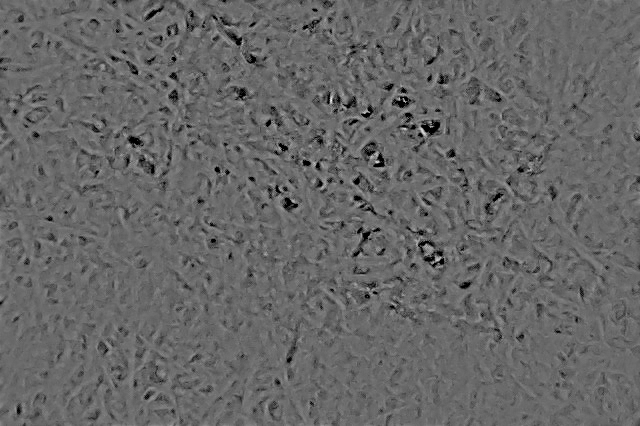
As you can see, this removed a lot of the variations caused by creping or shadows.

Some other footstep I took is to blow out the image resolution past a factor 20 using an interpolation algorithm. This allows me to measure pore sizes at the sub-pixel level, and obtain smoother pore size distributions with more data points in them. The next footstep to detect filter pores is to choose a threshold to separate a pore from the filter surface. I used a threshold of 0.5, which ways that any pixel darker than half of the epitome scaling is considered a pore. You can see visually what this results in, with all detected pores marked in red:

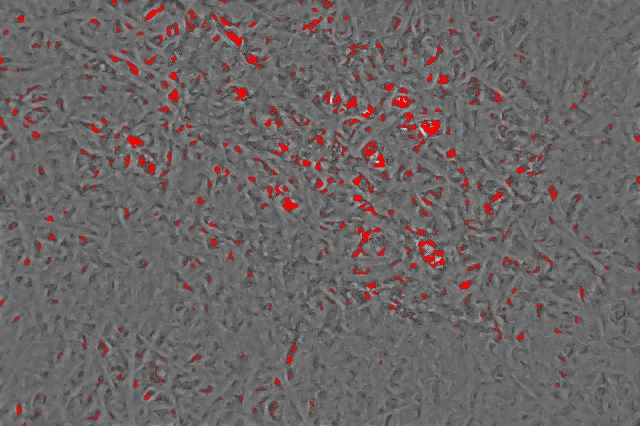
At that point, I simply counted the fraction of pixels that were marked as pores in this image.

if you are not interested in the details of how I coded the structure of pore size distributions, you can skip the adjacent paragraph, and the equation !

To do it, I used the magic of infinite numbers in coding. In some coding languages, those are chosen "Non a Number" (NaN), and they tin either exist your worst enemies because they crash all of your software, or your all-time friends considering you lot always keep them in heed and ensure your codes don't crash when they are encountered. Believe me, they should be your friends, considering they open up a lot of nice coding tricks. 1 of these tricks is the following: You tin create a mask prototype that has a value of 0.0 at every pixel respective to the filter surface, and NaN at every pixel where there is a pore. Y'all can then apply some fast and well-vetted box-smoothing algorithms to look at the larger scales in the image, and this will crusade the filter surface to slowly creep in and close down the detected pores.

Do this with many dissimilar smoothing box sizes (let'due south phone call such a box size x), and you will proceeds information on the fraction of filter pores at every size ! Another neat trick most the dynamics of how NaN values creep inward is that they will give y'all a list of pixel locations where square particles of a maximum radius of exactly x tin can pass through the pores; normal smoothing algorithms would underestimate what size of particles can pass because they would blur the edges of filter pores. If you count the fraction of masked pixels (let's call that m) for every box smoothing size (recall that we named this 10), it can exist demonstrated mathematically (I will spare you the details) that the distribution of pore radii f(x) is related to the second derivative of the masked fraction versus smoothing box size:

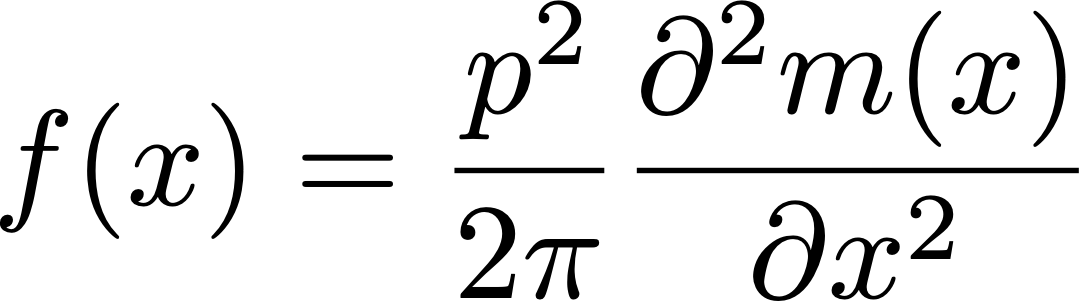
where p is the pixel calibration (in pixels per micron).

Basically, how much the fraction of masked pixels changes as you are smoothing the prototype gives y'all an indication of how much pore surface is beingness airtight down.

I found this algorithm efficient to quickly measure pore sizes regardless of their shapes beyond the image, and measuring grand(x) is basically asking "If you lot take ane squared particle of radius ten, what is the fraction of surface positions where it could pass through a filter pore ?"

These calculations resulted in a pore size distribution for each microscope image that I obtained. I and so combined the distributions from every epitome of a given filter to an average pore size distribution for that type of filter. I displayed pore diameters rather than radii, because I suspect this is what most people will assume if they hear "pore size". Here'due south an example of what I obtained with the Hario tabbed paper filters:

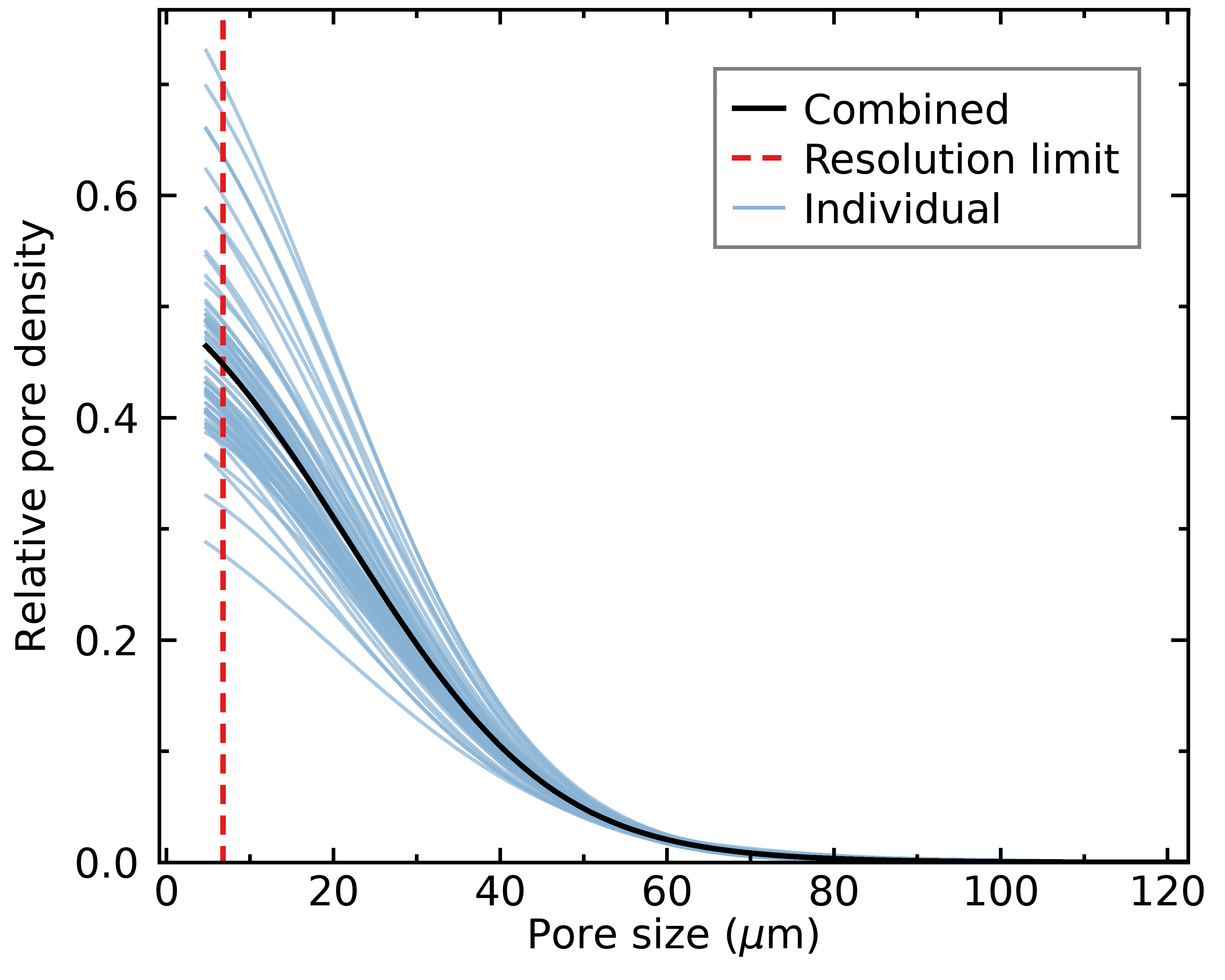
As you tin see, the peak of the distribution in terms of number of pores seems located beneath the spatial resolution of the microscope, but we will see later that this is not an issue given that we are interested in how the pore distribution affects flow rate, and we will see that the pores smaller than 10 micron take an insignificant contribution to flow for all the filters that I tested.

Here's how the distribution of each filter compared:

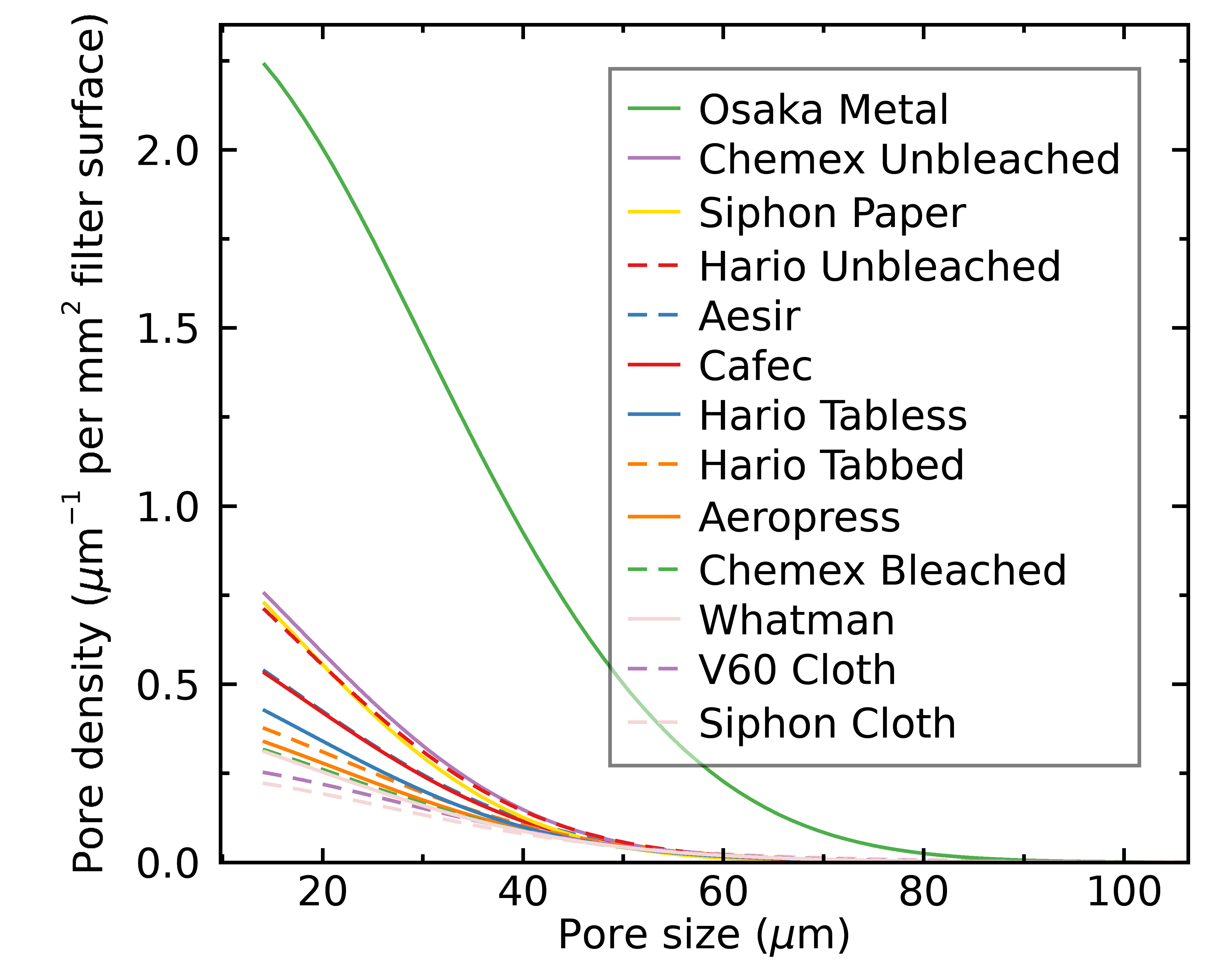
As you tin see, the Osaka metallic filter has mode more pores than the other filters. I find it more interesting to compare the normalized pore distributions, and to group them by brew method:

Pour Over

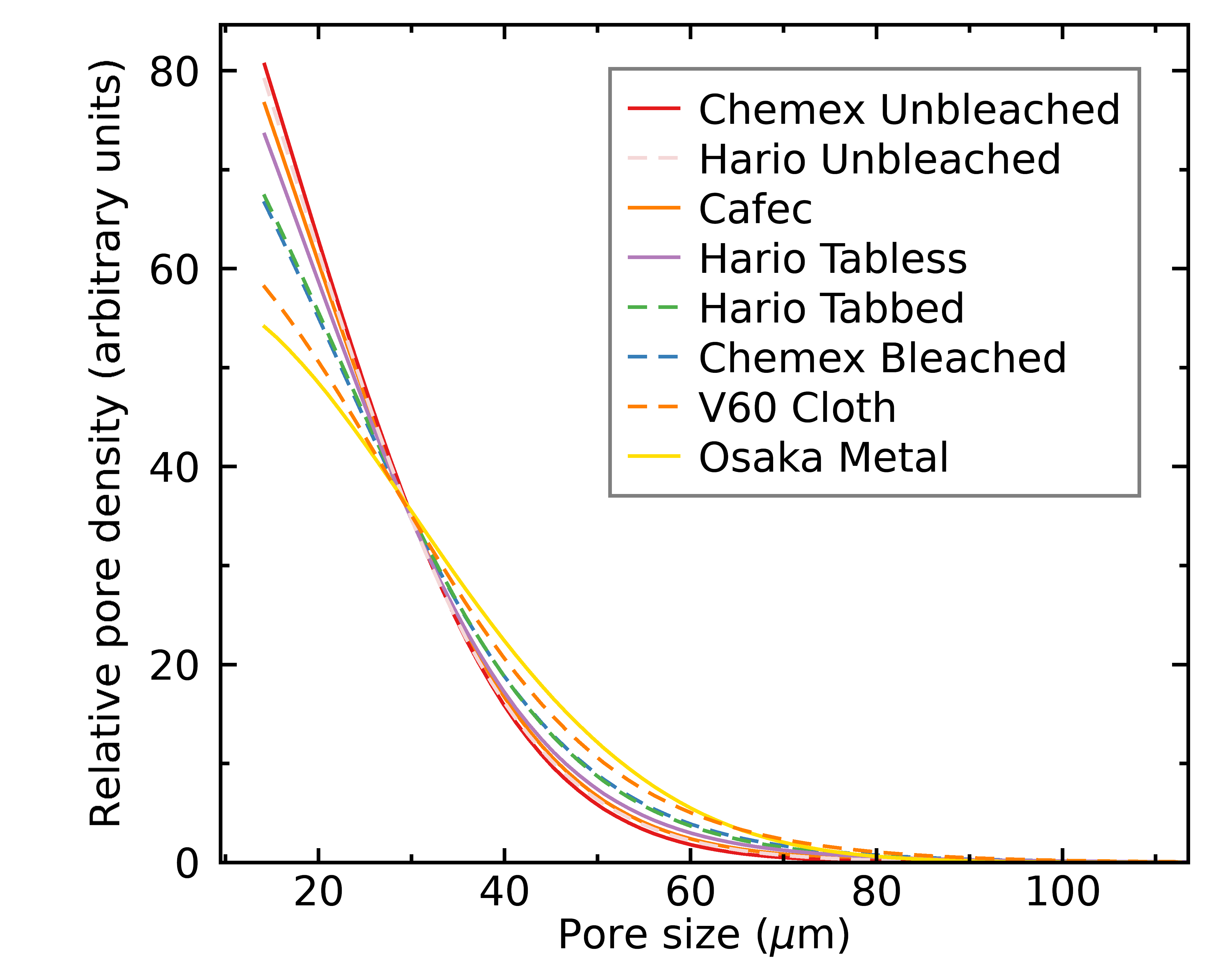
Aeropress

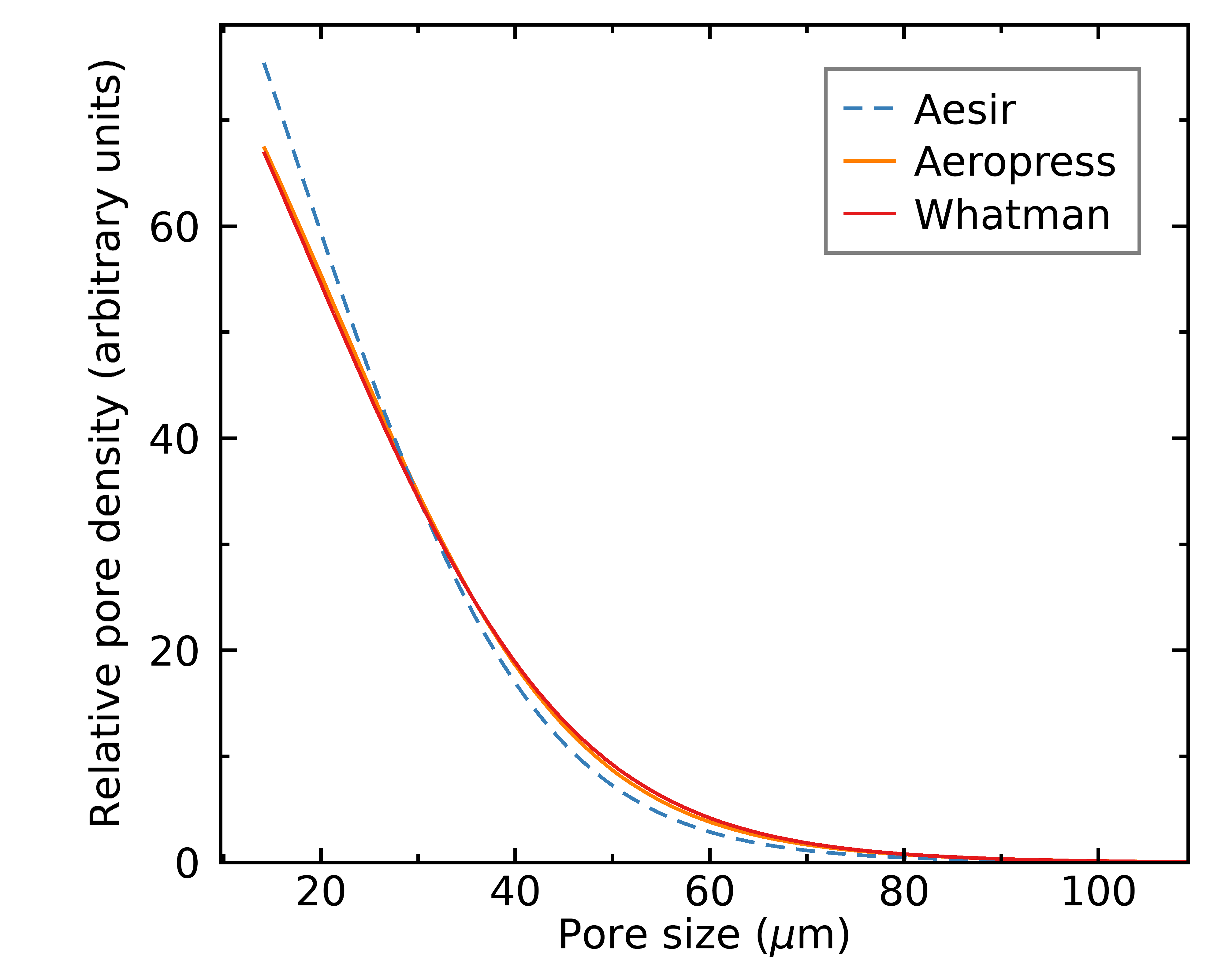
Siphon

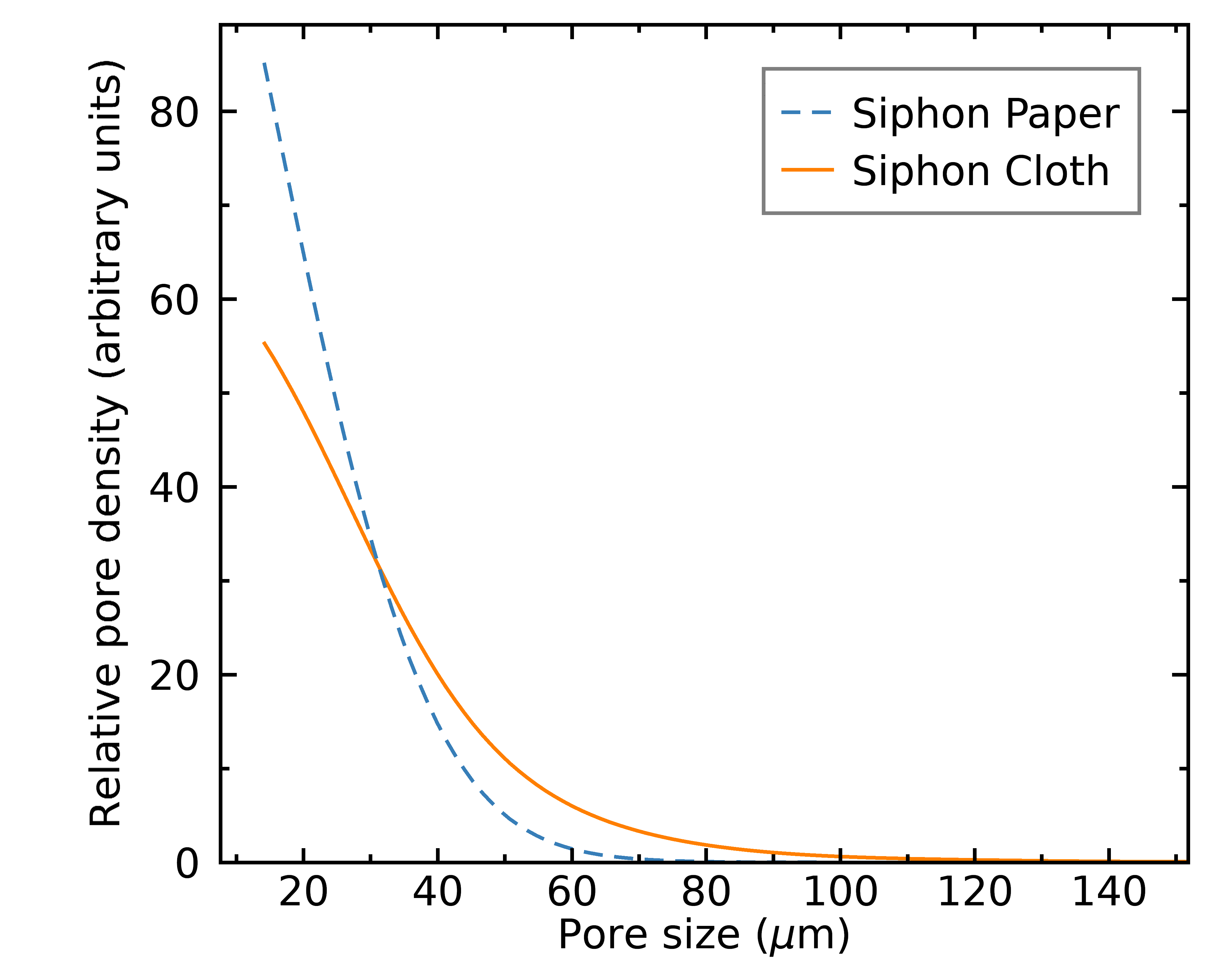
As y'all can run into from the distributions above, paper filters tend to take more uniform distributions in pore sizes (the slopes of the distributions are steeper). One thing I found actually interesting is that all unbleached filters seem even more uniform. This hints that the bleaching process may be affecting the pore distributions of filters, perchance in a way that will injure brew quality, but we'll come dorsum to this after.

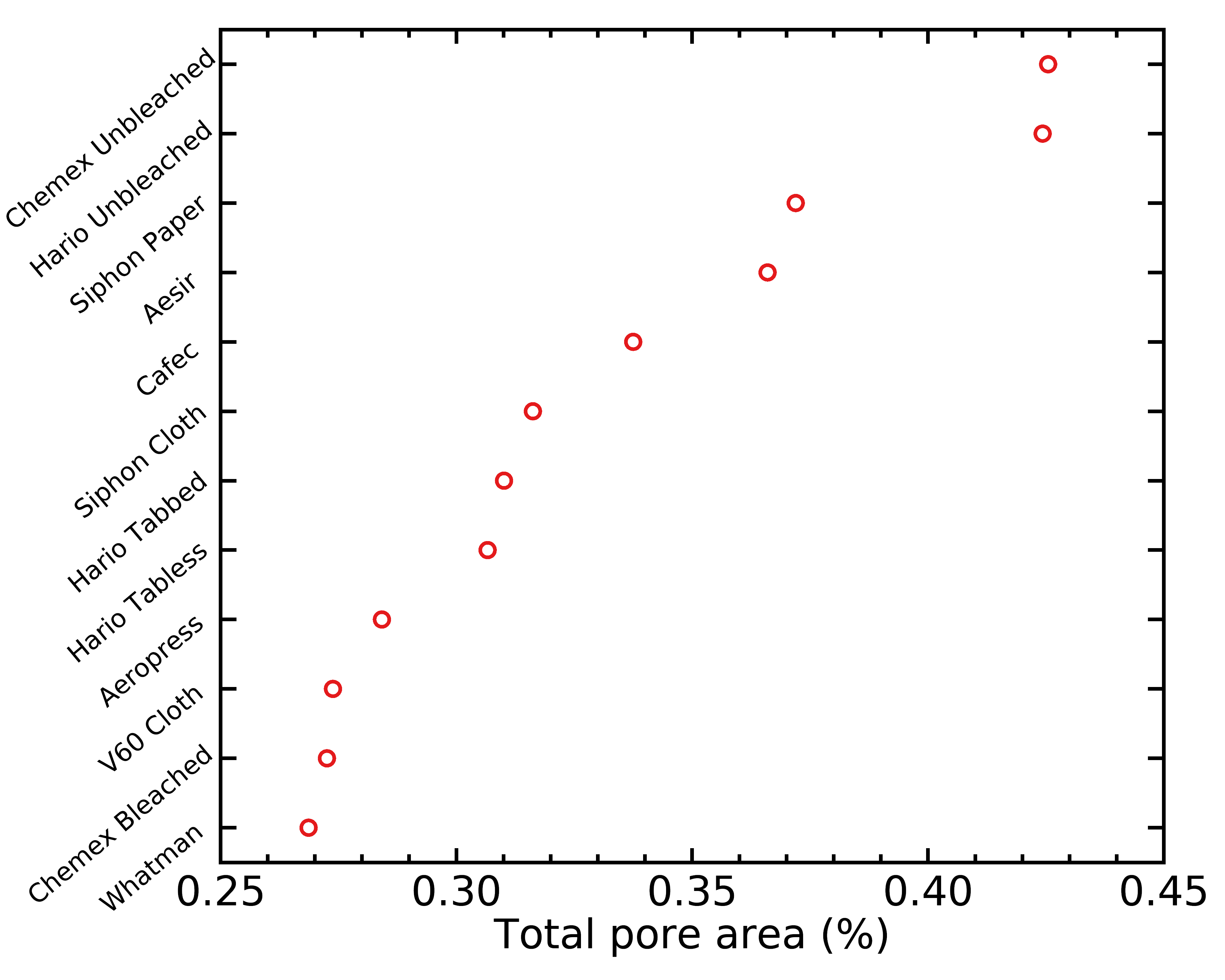
The units of the distributions above tin seem a scrap confusing, as they are in number of pores per micron per millimeter squared. The "per micron" part is caused past these distributions being probability densities, i.east., you demand to integrate their expanse under the curve to obtain a real number of pores, which will remove the "per micron" unit. The "per millimeter squared" is just the surface of the filter. If yous integrate all of these distributions across all possible pore sizes, for example, you could count how many pores per millimeter each filter blazon has. With a slightly dissimilar functioning, you can besides calculate the fraction of each filter'southward surface that consists of pores (I removed the metallic filter to get a clearer figure):

Filter Thickness

It is obvious from manipulating all the filters higher up that they have very different thicknesses. This is an important property of filters because it will impact their flow rates. I thus ordered a digital Caliper with a 20 micron precision to actually mensurate the thickness of every filter. Precisely measuring the thickness of a paper filter is really non as straightforward every bit you might retrieve; if you shut the Caliper too hard, the filter will get compressed and potentially damaged, and you won't measure out a realistic thickness in the context of water flowing through the filter.

To overcome this problem, I gently closed the Caliper on each filter to obtain a more than realistic thickness, just this brings up a whole new problem of measurement reliability. Fortunately, I can easily repeat these measurements many times on different filter locations, and different filters, and so I kept taking measurements until my fault on the boilerplate thickness became much smaller than the quoted 20 micron precision of the Caliper. Stats geeks volition know that this error on the average tin be calculated with the standard deviation of all values divided by the square root of the number of values.

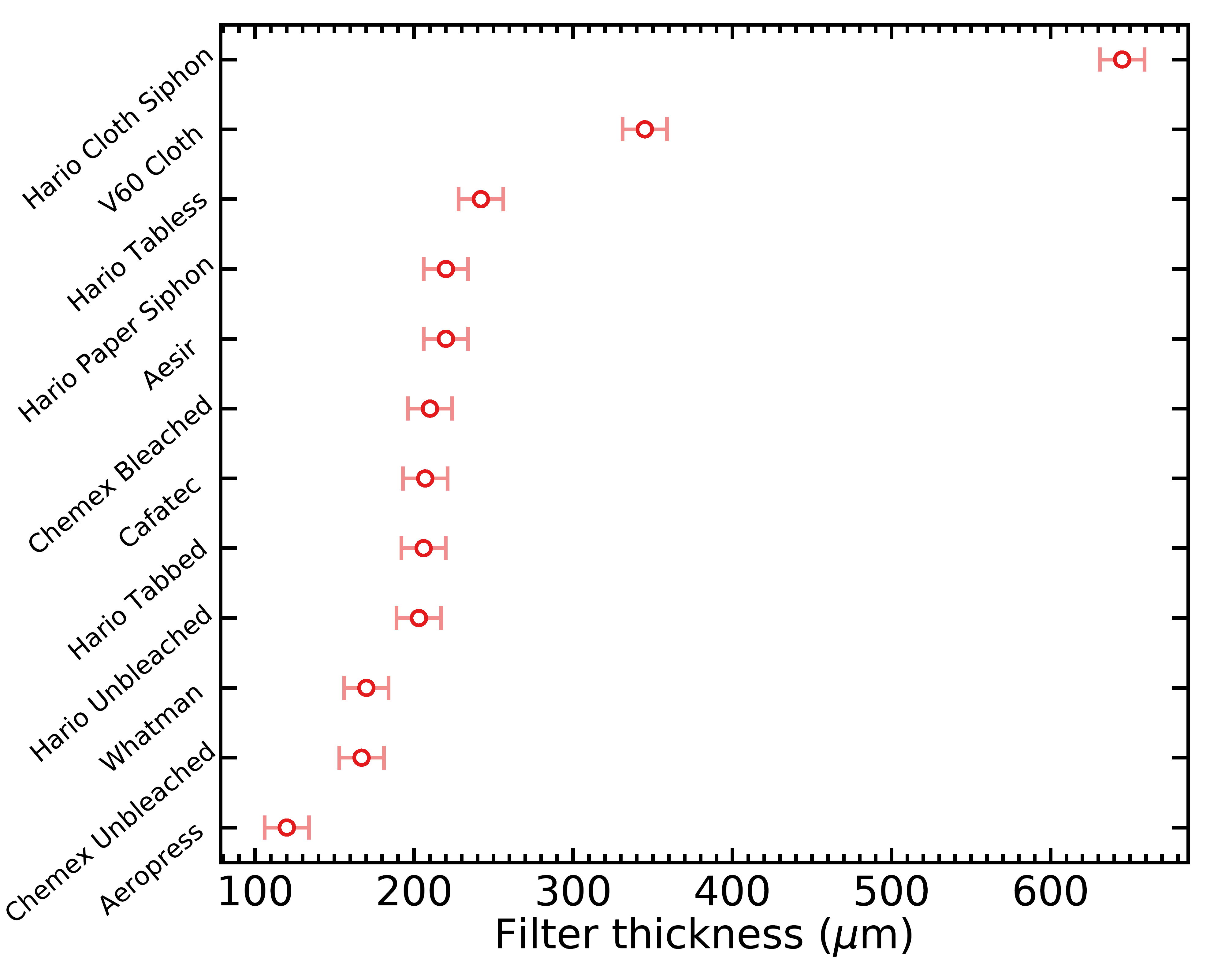
I ended up taking a total of over 700 thickness measurements (across all filter types) before I was confident in my results. Hither's the listing of filter thicknesses what I obtained:

Chemex unbleached: 167 ± 23 μm
Chemex bleached: 210 ± 22 μm
Hario unbleached: 203 ± 21 μm
Hario tabbed: 206 ± 21 μm
Cafec: 207 ± 21 μm
Hario tabless: 242 ± 22 μm
V60 fabric: 690 ± 22 μm
Aeropress: 120 ± 22 μm
Whatman: 170 ± 22 μm
Aesir: 220 ± 22 μm
Siphon newspaper: 220 ± 22 μm
Siphon cloth: 645 ± 22 μm

And here's the same data, displayed as a figure:

Filter Flow

Some other of import point well-nigh filter properties is how fast water flows through them on average. This is afflicted by factors like pore size distribution, filter thickness, but also their rigidity and how well they stick to the surface of a V60, because a better sticking filter volition boring downwards the upward escape of air and therefore slow downwardly flow. Because flow rate is a office of many circuitous and intertwined factors, I also measured them with a unproblematic experiment further down.

Nosotros tin can however make a prediction of menstruation rate, based on an arcadian planar filter with a compatible thickness and round holes. The theory behind it is given in some details here, but basically the only part you need is this one:

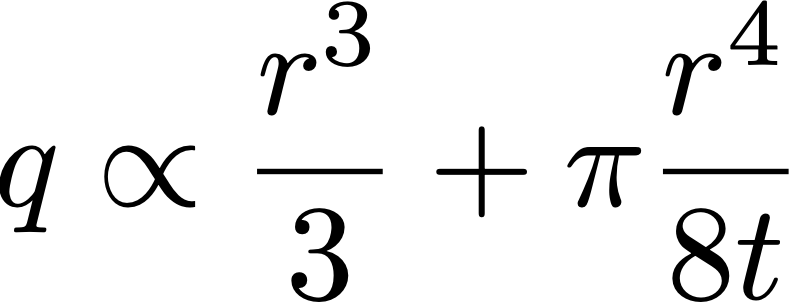
where q is the flow charge per unit in volume of water per second through a pore, r is the radius of the pore, and t is the thickness of the filter. The hidden proportionality constants are related to the force per unit area drop higher up and below the filter, and the viscosity of water. The beginning term in the third ability of r is called the Sampson term, and corresponds to the case with a filter much thinner than its pore sizes. The second term is chosen the Poiseuille term, and corresponds to a case where the pores are really tubes much longer than their bore. This combination of the 2 extreme cases is not perfectly exact, just it'south much simpler than the real solution, and it's always a valid approximation within 1% of the real value.

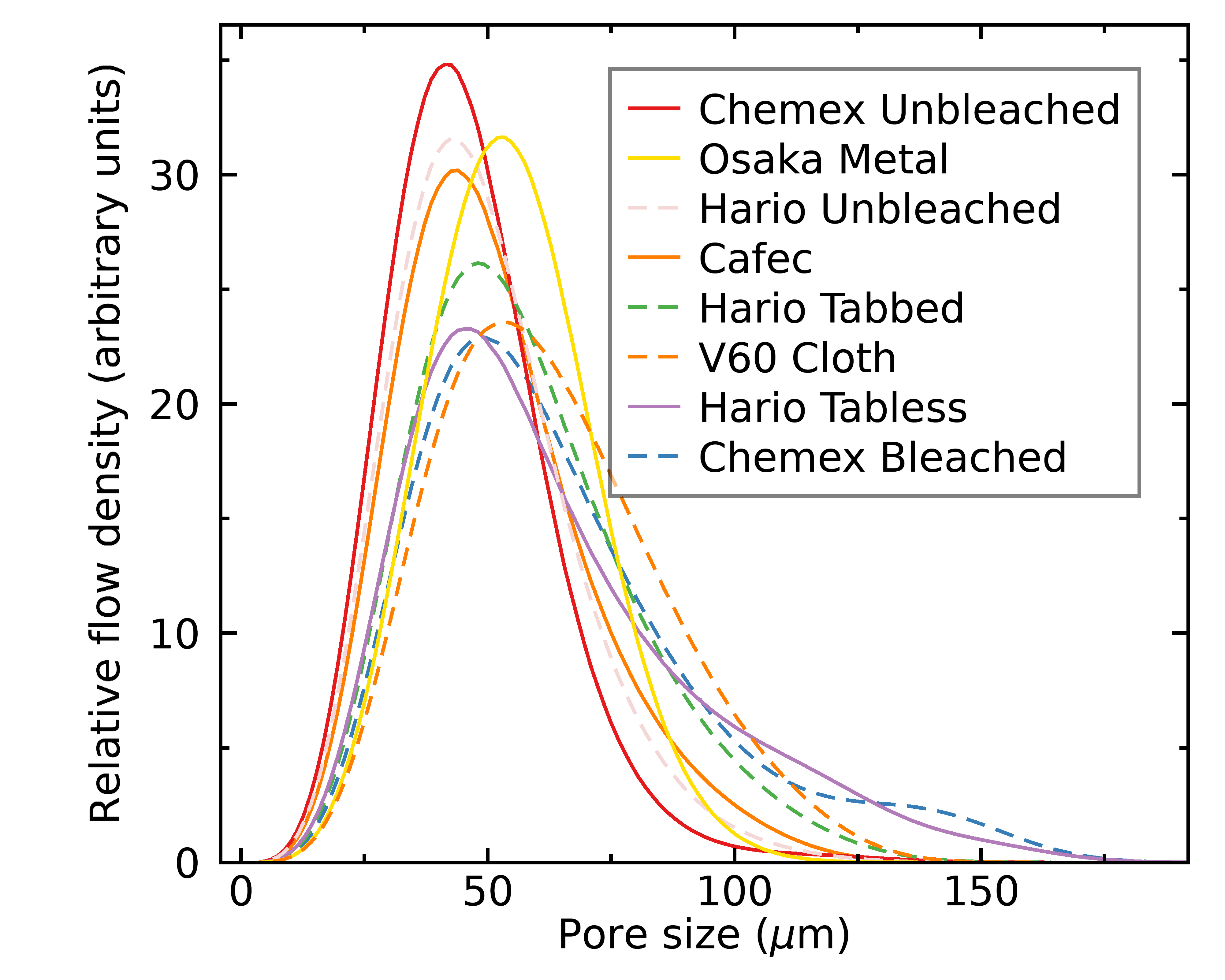
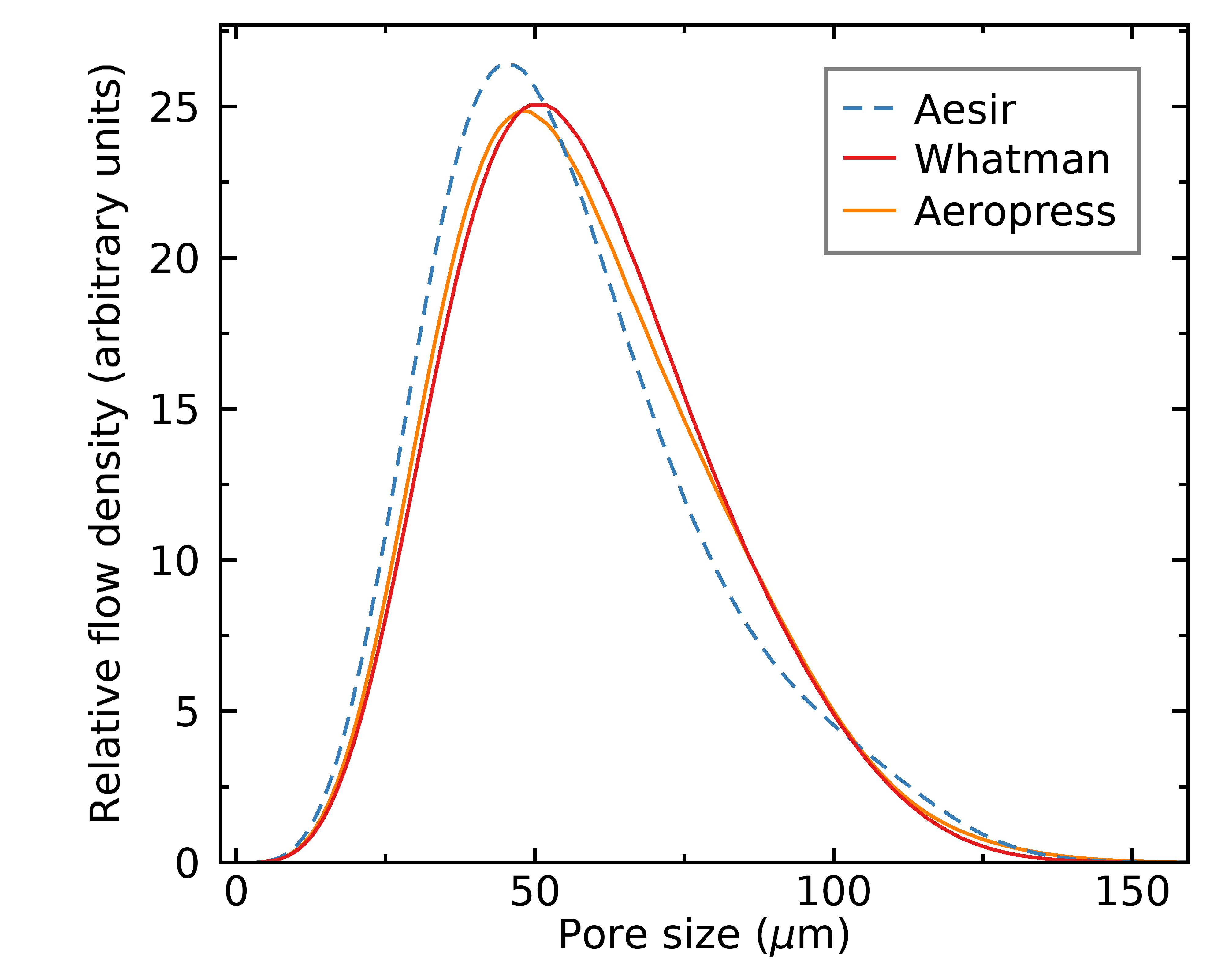
We can use the equation above to transform the distribution of pore sizes into a distribution of flow, and past integrating the full distribution nosotros tin estimate the full idealized flow rate for each filter. Hither's what I found, grouped by mash method;

Cascade Over

Aeropress

Siphon

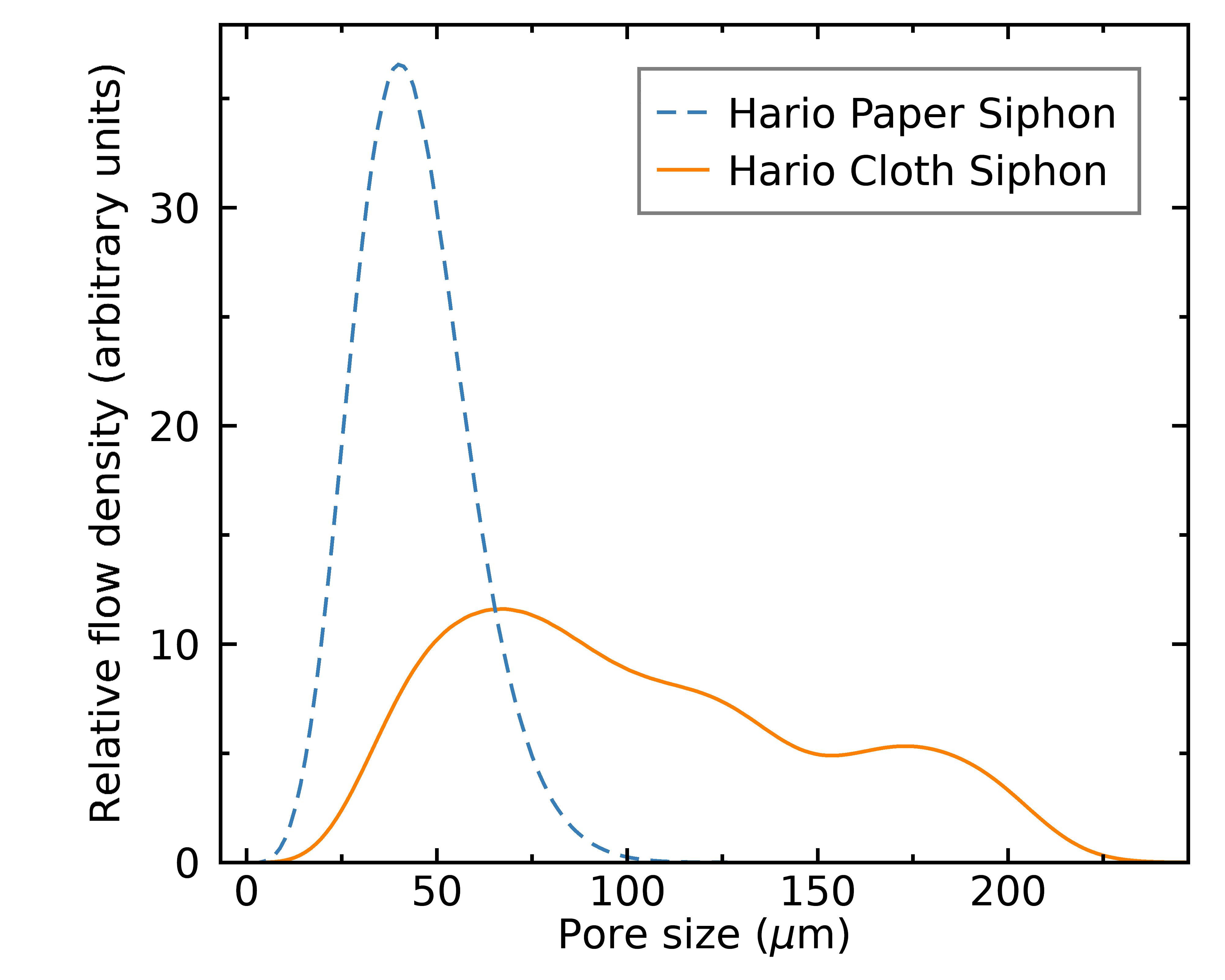
As y'all tin can see from the figures above, pores above ~xx micron are responsible for well-nigh of the catamenia in all cases. This ways that my microscope resolution (each pixel is vi.8 micron) is able to resolve the holes most relevant to empathise the catamenia dynamics. You might be surprised that the positions of the Hario tabless vs tabbed newspaper filters were swapped compared to the pure pore distributions (i.e., Hario tabless seemed a flake more uniform in terms of pore sizes, but less uniform in terms of menstruation); this is because the tabless filters accept a slight over density of very large pores, which are much more than important than small pores when nosotros talk about flow. Hence in practice, this makes the Hario tabbed filters seem slightly preferable.

Here are the total idealized flow rates for all filters, obtained by integrating the flow rate distributions above:

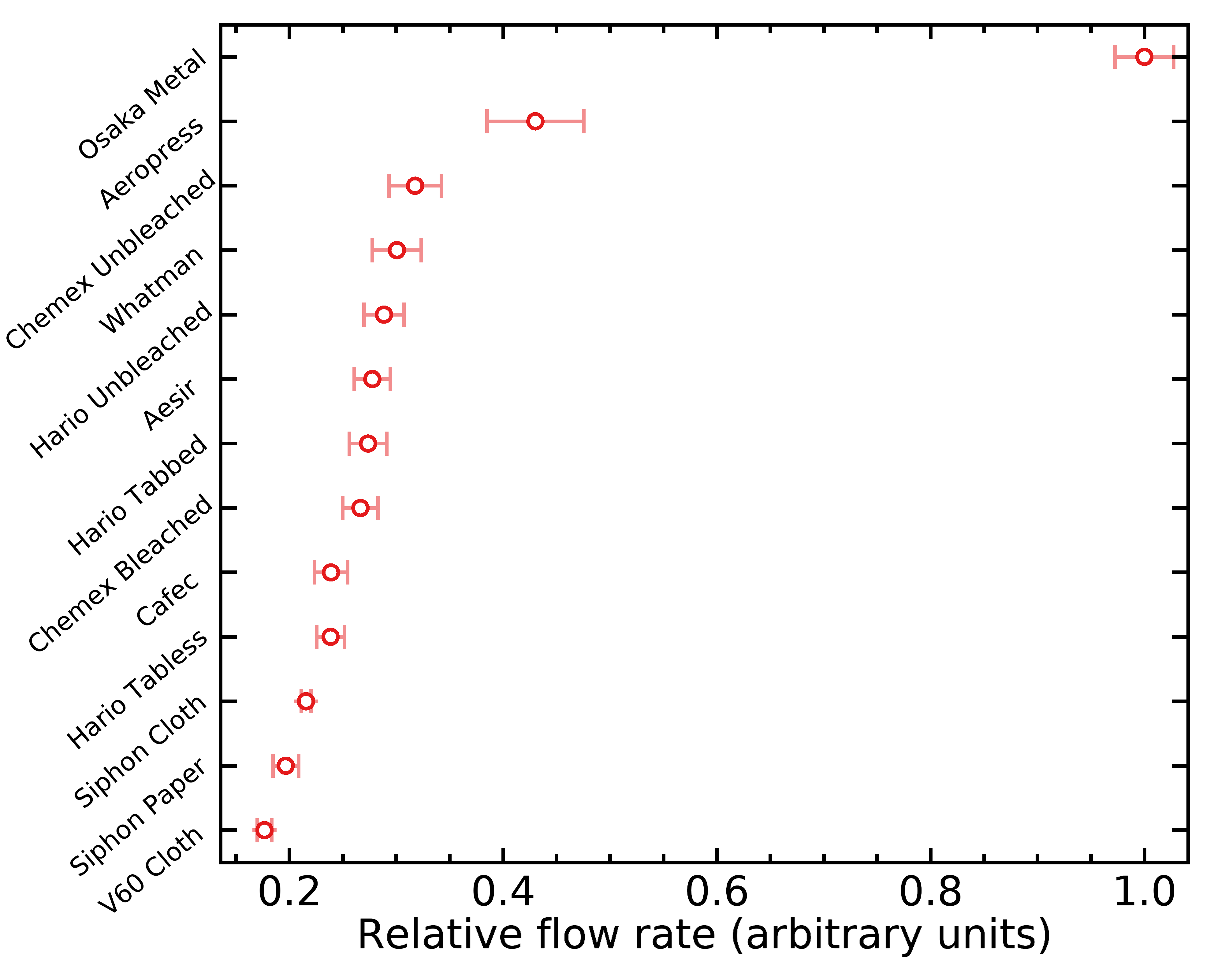
After calculating these idealized catamenia rates, I went ahead and measured the real menstruation rates of all pour over filters above. I took the immersion dripper switch from Hario, put a filter on information technology and stuck a marked chopstick in the filter. I used 150g room temperature (25°C) distilled water to pre-rinse the filter so that it sticked to the V60 walls, turned off the switch so that it doesn't flow, and added some other 150g of room temperature distilled water.

I used an iPhone chronometer which allows you to place your finger on the "starting time" button and it actually only starts when you release your finger; this makes it easier to trigger both the Hario switch and the chronometer at the aforementioned time. Once the switch was opened, I used the iPhone LED calorie-free to pay conscientious attention to the water surface and I striking the chronometer again when it passed the blackness mark on the chopstick. I took 6 measurements per filter; this immune me to get a better measurement and estimate my measurement errors with standard deviations. Here are the resulting filter flows:

Cafec: 5.79 ± 0.03 mL/sec
Hario tabless: 6.89 ± 0.05 mL/sec
Hario tabbed: 11.03 ± 0.02 mL/sec
Hario unbleached: 15.three ± 0.1 mL/sec
V60 Textile: eighteen.1 ± 0.3 mL/sec
Osaka metal: 67.8 ± 0.six mL/sec
Chemex bleached: 7.23 ± 0.02 mL/sec
Chemex unbleached: nine.82 ± 0.02 mL/sec

The detailed data are available here. Continue in mind that flow tin can exist afflicted past water viscosity, your grind size, filter clogging, etc.; so these values are most interesting when compared to each other in a relative sense. The error bars are mostly due to my ability to start and stop the timer at the correct time; my standard divergence on timings across all filters was 0.2 seconds, and manifestly the average human reflex delay is 0.25 seconds, so it seems credible that the reflex inconsistency be of that same lodge of magnitude.

Now let'southward compare the idealized versus predicted menses rates, and run across if they correlate well:

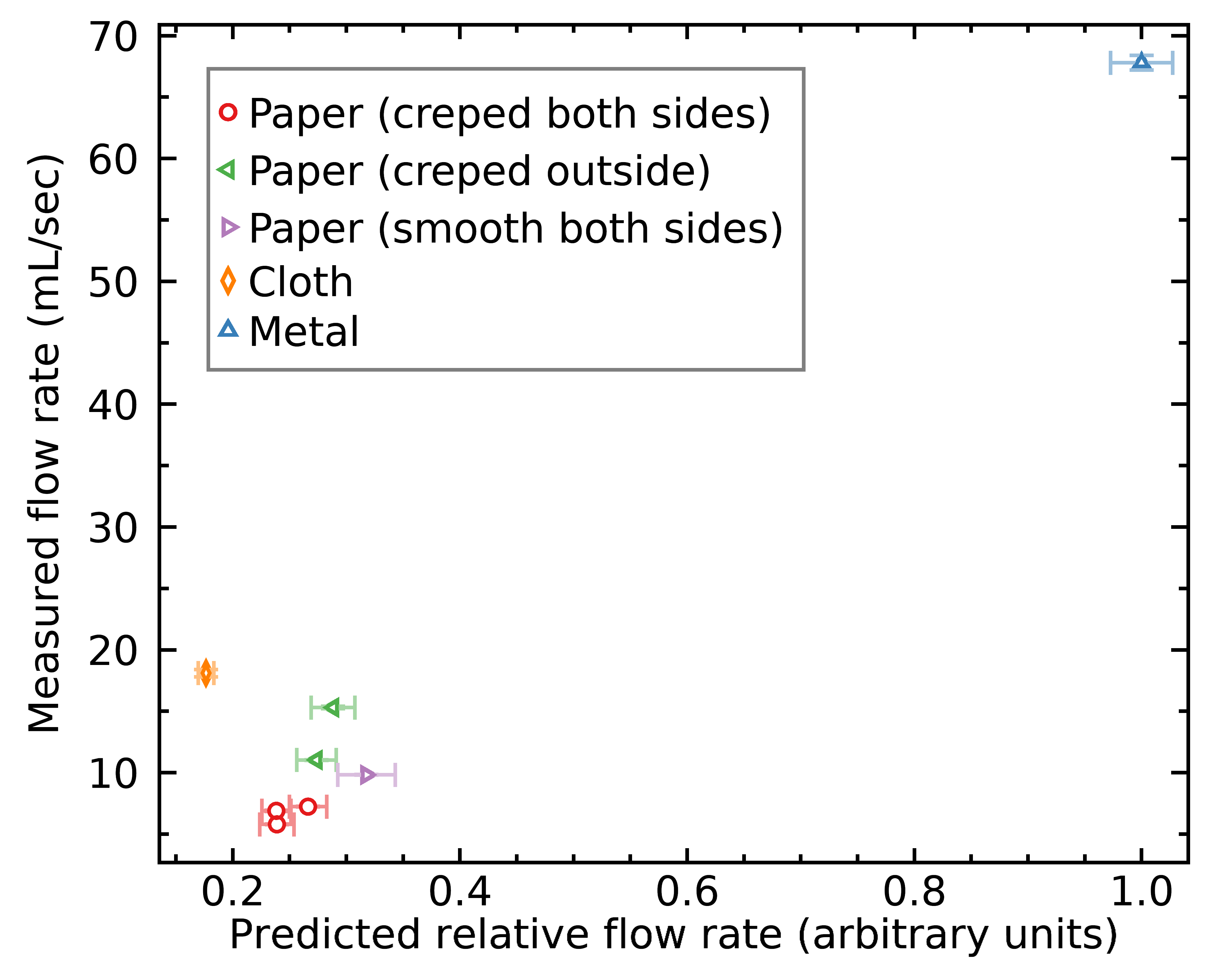
If the idealized menses rates were perfect, all filters would fall along a straight line in this figure. As y'all tin can see, it is not the case at all; it seems that filters made of unlike materials or with different creping behave differently. I think this is due in role to how they adhere to the walls of the V60, but I think that creping inside the filter may likewise contribute to slow down menstruum because water will prefer to menstruum by and large along the crepe valleys instead of everywhere on the filter surface. If that's true, then filters smoothed on the within would be preferable, equally they would promote a more uniform flow across the filter surface. I won't exist able to make up one's mind whether that's true or not with any more certainty in this postal service.

Another hypothesis I had is that the pores of newspaper filters may be better represented by diagonal tubes instead of straight upwardly ones, in which case the "effective" thickness of the filter would always be a factor larger than their truthful thickness. While this may exist true, I observed no clear correlation between filter thickness and how offset the idealized flow rate was from the existent period rate; this indicates that this effect is non the biggest cause for these differences.

The Tainting Issue of Filters

Some other often discussed cistron about coffee filters is how they might straight affect the taste of a coffee beverage by contributing chemic compounds to the coffee potable. This is what can produce this undesirable papery or cardboard gustatory modality, and is often the quoted reason for why pour over filters need to be rinsed before brewing. To be sure, there are other reasons to exercise it; pre-heating the brewing vessel and making certain the filter is well positioned in it are also important reasons why we pre-rinse cascade over filters.

I once did a preliminary experiment where I pre-rinsed Hario tabless and tabbed filters (both are bleached) and then immersed them in hot water for a few minutes, and tasted the h2o. I was non able to confidently say that I could sense of taste annihilation different from just the tap water, so I ended that I could use either of them without worrying near sense of taste, at to the lowest degree if I pre-rinsed them.

Simply there is a more objective way to compare how much each different filter can taint your coffee potable, with distilled water and an electric electrical conductivity (EC) meter that measures total dissolved solids (TDS) in h2o. I decided to measure those by emulating a water temperature, contact fourth dimension and water weight that are like to typical brewing conditions. I put the dry out filter in the Hario switch pour over device, turned off the menstruation, and poured 200.0g of distilled h2o (1 ppm) in the device, weighed with a 0.1g-precise brewing calibration. I didn't utilize more than 200g to avoid over-filling it. I so immediately put a cork lid on meridian of it for oestrus insulation, and waited iii minutes earlier I turned on the flow switch.

I then placed the water in a minor ceramic loving cup, which I covered with a plastic lid to stop evaporation. I waited a few hours until the samples came close to room temperature (I measured them at 27°C, and the room temperature was 25°C). I decided 27°C was ok considering the TDS measurements had stopped changing betwixt 40°C and 27°C, and waiting for the samples to cool more would have taken hours more notwithstanding. The EC meter that I used applies a temperature correction, but it is non perfect so it's all-time to remain within a few degrees of 25°C to get absolute TDS measurements. I fabricated sure that all samples were measured exactly at the same temperature (27°C). To these measurements, I subtracted the 1 ppm solids that were already there in my distilled water. Here's what I obtained:

Hario tabbed bleached: 0 ppm
Hario tabless bleached: 0 ppm
Cafec bleached: 1 ppm
Hario unbleached: 5 ppm

As you lot can meet, bleaching actually does what it's supposed to do, but for some reason, the Cafec filters seem to still have a small corporeality of dissolvable compounds left in them. These measurements are consistent with my being unable to taste any effect of the bleached filters in a water immersion, especially given that I had likewise pre-rinsed them. This also seems to lend credence to Scott Rao who didn't pre-rinse the Aeropress or Whatman filters that he places on superlative of his high-extraction espresso pucks.

This all seems like a cautionary tale confronting using unbleached filters, but what I was testing here is the inherent power of these filters to taint your coffee beverage if you don't pre-rinse them. As I mentioned earlier, tainting is not the only reason we pre-rinse pour over filters, so I would certainly not recommend y'all finish pre-rinsing bleached filters, but there are scenarios like an upper espresso puck filter where pre-rinsing might not thing. Now what would be fifty-fifty more interesting to me is to ask a more than practically applicative question: what happens to these numbers if we pre-rinse the filters ? And how much do we need to pre-rinse them ?

To answer these questions, I carried a different experiment that resembles two of the filter rinsing techniques that I used, applied to the Hario unbleached filters as a worst case scenario. The goal of these experiments was to see whether I can notice any additional dissolved solids imparted by the filter.

The first rinsing technique that I most often employ is to first pre-rinse with cold tap h2o, because brew water is a scrap more precious. I then pour a little flake of hot mash water to preheat the vessel, which is probably not that important as I use the plastic V60, but besides to supercede h2o suspended in the filter with my brew water that has the desired alkaline buffer. This is probably a bit overkill as the amount of retained water is small-scale, only it's an easy matter to do.

For the beginning experiment, I therefore used room-temperature distilled water (one ppm) with the Hario switch, but this time I left the menstruum switch open. I poured three pulses of approximately 50 grams of water into three singled-out cups, and then a final pulse of hot distilled water in a small ceramic container. I covered the ceramic container with a plastic lid and allow it cool down to room temperature, and so that I would get a more accurate TDS reading with the EC meter. Here's what I obtained, after subtracting the initial 1 ppm to every measurement:

First cascade (dry filter): Poured fifty.iii g water, resulted in five ppm TDS in 47 k output, i.e. 3.three g h2o was retained by the filter and 0.235 mg of filter textile was dissolved.

2d pour: Poured 49.7 g water, resulted in 3 ppm TDS in 48.v g output, i.due east. 1.2 one thousand water was retained and 0.146 mg of filter material was dissolved.

Third pour: Poured 49.9 1000 water, resulted in one ppm TDS in 49.6 m output, i.eastward. 0.three thousand h2o was retained and 0.050 mg of filter fabric was dissolved.

Fourth pour (hot water): Poured 49.8 g hot water, resulted in i ppm TDS in 49.8 chiliad output, i.e. no h2o was retained and 0.050 mg of filter textile was dissolved.

This indicates that tap water removed about of the filter materials, but switching to hot h2o allowed to extract a tiny bit more than, although I would be skeptical that 1 ppm of filter materials could be humanly tasted. It also seems that the filter was able to retain a total of 4.8 thou water and contribute 0.481 mg of paper material.

For the second experiment, I used a similar method simply used only hot water, and used 100 grams for my initial pour because I knew 50 grams would non be plenty to remove all filter solids.

Start pour (dry filter): Poured 100.0 k hot water, resulted in 10 ppm TDS in 95.viii chiliad output, i.due east. four.2 thou water was retained and 0.958 mg of filter material was dissolved.

2d cascade: Poured 49.6 g hot water, resulted in 6 ppm TDS in 48.8 g output, i.e. 0.6 g water was retained and 0.293 mg of filter material was dissolved.

Third pour: Poured 49.3 g hot water, resulted in 0 ppm TDS in 48.v one thousand output, i.e. 0.8 chiliad water was retained and no detectable filter fabric was dissolved.

In this case, it seems clear that 150g of hot rinsing h2o was enough to deplete the filter of all dissolvable materials. The filter seems to have retained a full of 5.6 grams of water, which is a bit more than than the previous one. I don't think this is due to the water being hot, but probably to how fast I moved the V60 when I picked information technology upwards. In this case, a total of 1.251 mg of filter material was dissolved, more than double what was dissolved in the starting time experiment. It'south therefore preferable to rinse unbleached filters with hot water, otherwise y'all'll probable need a large corporeality of water. This is non true of whatsoever bleached filters; as you may recall, even the first pulses of water contained no dissolved solids.

Uniformity Alphabetize

One filter property that I expect could help achieve a uniform cascade over extraction is how consequent the flow is beyond the surface of the filter. If pores are grouped in some regions of the filter, this will contribute to channeling, i.due east. water will have preferential paths across your coffee bed and won't extract in a very uniform manner. To guess this effect on the various filters I investigated, I calculated the total idealized flow in each microscope image that I took for a given filter and looked at the standard divergence of these values for whatever given filter. If a filter always seems to have a like flow regardless of the position where I placed the microscope, that is a great thing, and it means that channeling should exist minimized.

I defined the uniformity index (UI) just as the changed of the standard departure of unit-less idealized flow across filter regions; this mode, a college UI corresponds to a more uniform filter. I did non assign any concrete units to this alphabetize because information technology would require specifying the water viscosity, pressure level driblet across the coffee bed, etc. Hence, this alphabetize is simply useful as a relative mensurate betwixt filters, and it could non exist compared with those calculated from any other pore detection algorithm or microscope. Here are the UI I calculated for all filters under consideration:

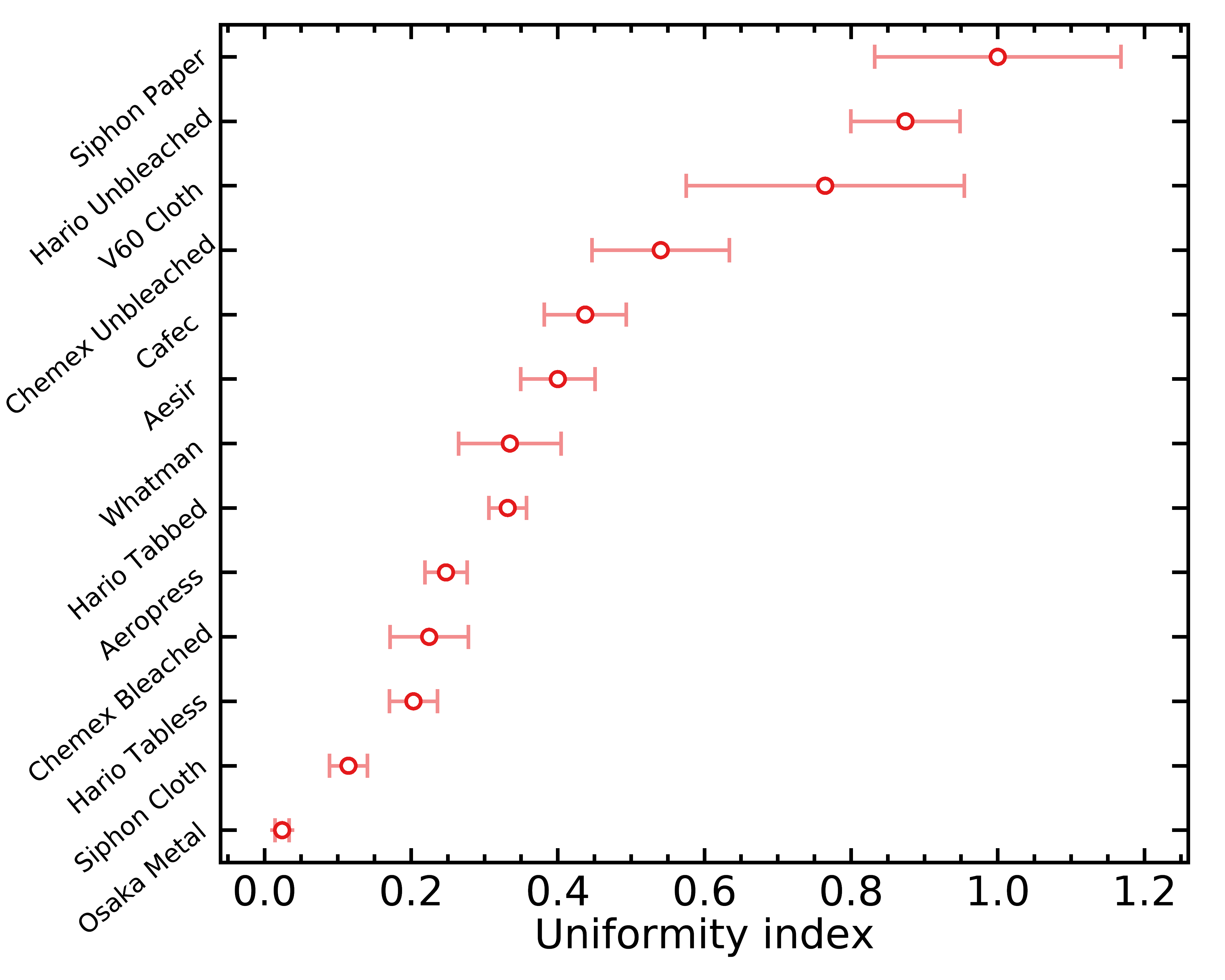
The error bars in a higher place are based on small number statistics. Remember that a higher UI is proficient; it means the filter will catamenia more uniformly across its surface. Notice how the unbleached filters come out at the pinnacle once more !

Equally I already mentioned, I suspect that filters with a higher UI may produce a more uniform extraction, maybe even more than and so if yous utilise minor doses in your pour overs. Even so, what I do not know is the appreciable importance of this effect; the event could be too pocket-size to thing in practice. This all the same opens up interesting practical experiments; for example, it seems possible that the Hario unbleached paper filters may permit us to reach more even extractions, and that would event in a college boilerplate extraction yield when everything else is kept fixed.

Filter Bottleneck Index

A typical problem that one can encounter when brewing coffee is a sudden decrease in period rate acquired by very fine coffee particles clogging the pores of a filter. For this reason, the values of flow rate that I measured higher up must be taken with a grain of table salt: if a filter flows very fast considering information technology has very big pores, coffee fines might exist able to clog them, and as a result the filter menses charge per unit might decrease heavily during a brew, and depend strongly on your brew method (e.g. the volume of your bloom phase, whether yous stir the slurry or not, etc.). If the filter flows fast because it is thin, the decrease in menstruum rate might be less of import, and less sensitive to your technique.

Information technology is possible to calculate a clogging index in an objective way, by calculating the overlap between the pore size distribution of a filter and the particle size distribution of a grinder. Obviously, different grinders (and different grind settings) will produce different amounts of fines, just using any reference grinder will provide a valuable relative cess of how each filter is sensitive or not to bottleneck. The resulting clogging index will therefore be most important to consult when using a grinder that produces a larger corporeality of fines – in my experience, you mostly go more than fines with smaller burrs, conical burrs, or anything that can widen the full particle size distribution similar misaligned burrs.

Non anybody seem to adopt grinders that produce the everyman possible amount of fines (and then far, information technology seems to be my preference), but whatever your preference is, you should always try to avert filter clogging. A filter will typically not clog in a uniform and immediate way, and that means you lot will get channeling as water starts to follow some preferential paths along the un-clogged filter pores. As you lot might already know, channelling will over-extract java along the aqueduct paths, and cause astringency (a dry feeling in the rima oris) in the resulting mash. Therefore, if you use a grinder that produces more fines, you should consider using filters that have smaller bottleneck indices. On the other hand, if y'all use a grinder that produces very niggling fines, this might be less of import.

You might be aware that I wrote an app to measure particle size distributions, but I never used it in combination with a microscope, and without this it won't be possible to use it to build a particle size distribution down to particle sizes as minor as filter pores. In the future I will experiment with this, but for at present I opted to use a laser diffraction particle size distribution instead. This distribution was generously sent to me by John Buckman and Scott Rao, who brought a sample of the Weber Workshops EG-1 (version i) grinder with stock burrs to a laser diffraction device:

I used the spider web plot digitizer to extract data from that photo, and I calculated the clogging index of each filter by performing the following operation:

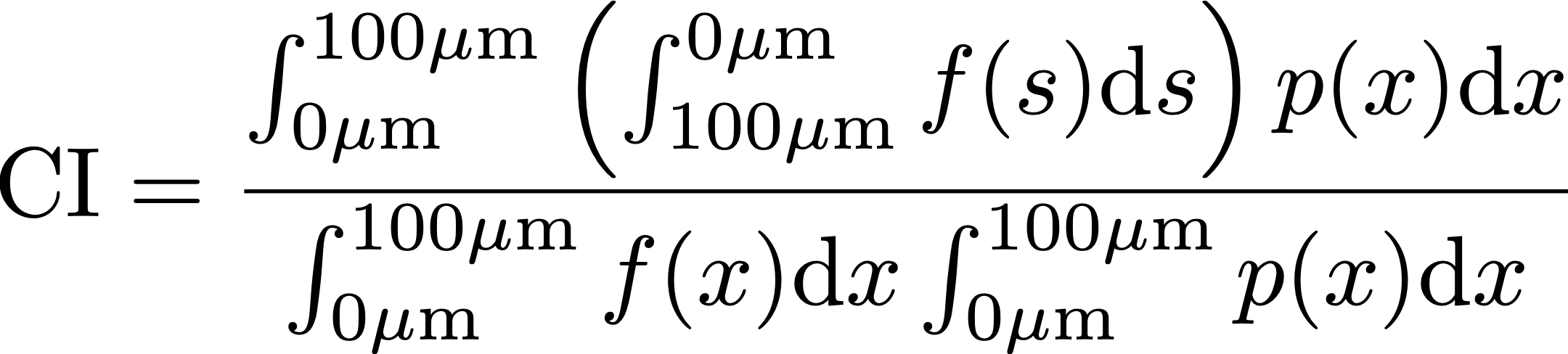
where f(x) is the pore size distribution of the filter and p(ten) is the laser diffraction particle size distribution of the EG-ane. The numerator includes a reversed cumulative density role of the pore size distribution because a coffee particle can contribute to clog whatsoever filter pore that is the same size or larger. Technically, the closest thing I'd know how to telephone call this operation is the integrated product of a cumulative density function with a probability distribution function; information technology's not a convolution.

If this looked similar alien symbols and sounded similar gibberish to you, that's totally fine. Hither's what it comes downwardly to: the clogging index is an estimation of the average fraction of period that tin can exist chock-full past coffee particles smaller than 200 micron in diameter (100 micron in radius). If CI = 90%, information technology means that the average coffee fine smaller than 200 micron would be able to cake pores that contribute ninety% of the flow rate for a given filter, if you use enough coffee and agitate information technology plenty. It does not correspond to the true fraction of flow that volition exist blocked by clogging, because that would depend on how much coffee you apply and how large your filter surface is; some fines may exist modest enough to cake 90% of the filter menstruum, only if they are not nowadays in large enough numbers to block all the pores, or don't always come in contact with the pores, then that won't happen. I don't desire to endeavor to brand these numbers representative of the true fraction of blocked catamenia, because non only it would become overly complicated, but it would as well not be accurate because java filters are not arcadian flat planes with circular holes. These numbers are notwithstanding very useful to compare filters in a relative sense, to understand which filters might clog more than easily than others.

Hither are the CI I obtained for all filters tested here:

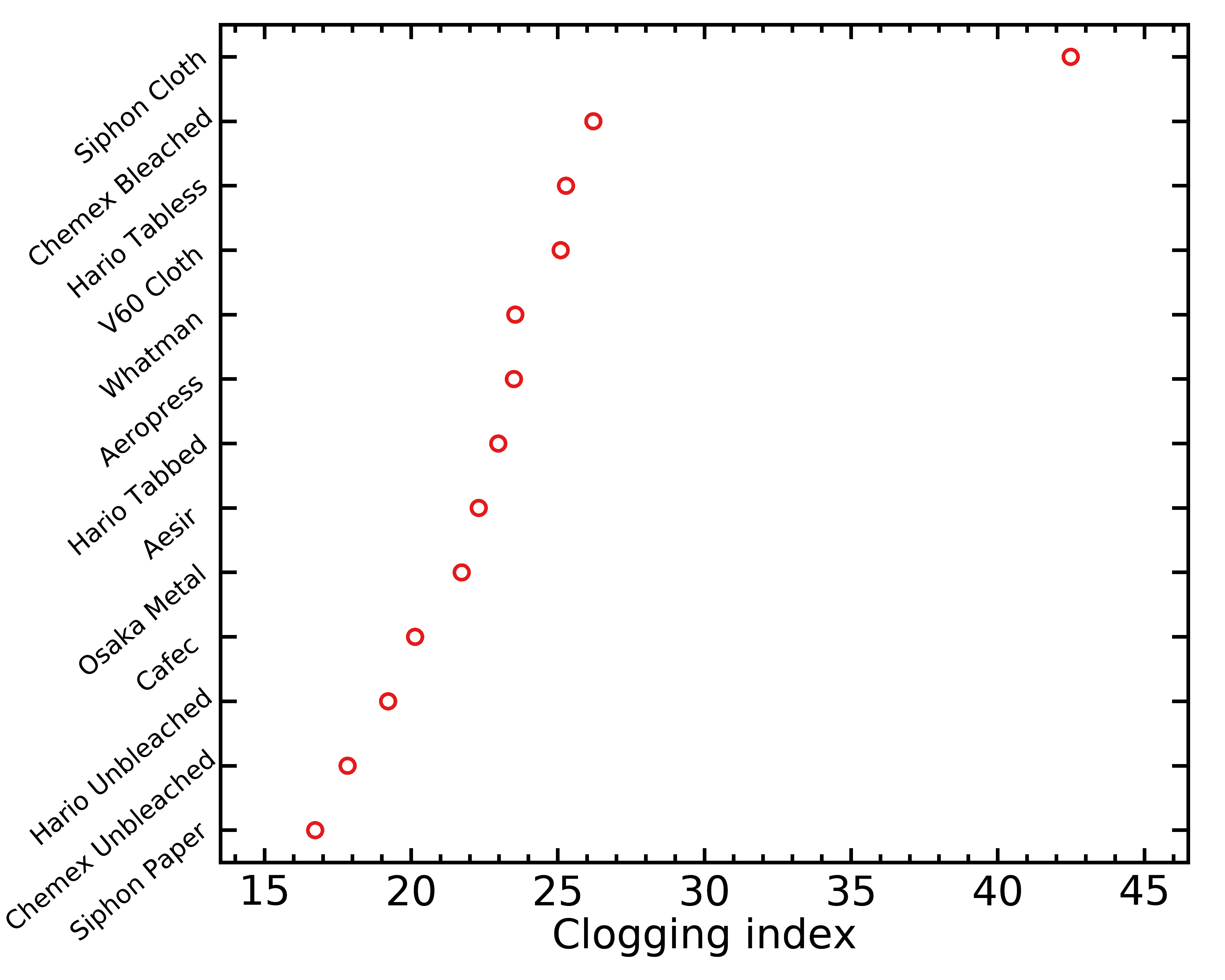
Remember that a small CI is practiced, every bit it ways your filter is less sensitive to clogging. The trend of unbleached filters coming up as the superior ones seems to hold yet over again !

Final Recommendations

I know this post contains a massive amount of data, then I'd like to dribble some of what I learned into applied recommendations. Please keep in listen that those are based on limited experiments, which comes with its caveats: for instance, it is possible that wetting the filters affects the pore size distribution, and it is possible that the more fifty-fifty pores beyond the filter surface only affects channeling in a very small layer of the java bed. Therefore the recommendations beneath should not exist taken as an absolute truth, but rather as a guide for what seems nigh worth exploring with your next V60 experiments.

Metallic Filters in General

Metal filters suffer from a major trouble in my opinion: the pores are typically and then big that the menstruum is only constrained by the grind size, and that will force y'all to grind very fine in order to obtain practical mash times. But this also means that a lot of fines will pass through the metal filter. Metal filters are also unlike from paper filters because they don't filter with mazes of spacings between paper fibers, only rather just straight, big holes through an otherwise very uniform and flat filter. Therefore, metal filters won't clog, and any fines small enough to penetrate the pores will end up directly in your drink. This means metal filters won't produce very clear brews like other pour over filters, instead they volition produce a beverage with suspended solids and fines, with less clarity and more body. Personally, I'm not a fan of this.

Textile Filters in General

Cloth filters endure from a similar trouble to the metal filters in terms of flow rate and large pores. Even so, they are in my opinion much worse because they are a hassle to properly make clean and re-use. I wrote a lot more near this in my post most a high extraction yield siphon recipe, and I'd encourage y'all to read it if you want more information about proper management of cloth filters, only I only gave up on using them.

Paper Filters for Pour Over

Paper filters are much more interesting to me, as their smaller pores allow to prevent java fines from passing into the beverage. The coffee bed does a lot of the job at retaining coffee fines, but if the filter had larger pores, some of them (either those already at the bottom or those that migrated downward) would still pass through.

Ane large take away point that I got from this analysis is that bleaching seems to deteriorate the quality of pore distributions. This is truthful in terms of the general spread in pore sizes, but even also in how much the flow of water varies across the surface of the filter.

This was surprising to me, every bit my initial bias was to disregard unbleached filters because of their tainting potential. But as we besides saw higher up, it seems possible to remove all dissolvable solids with an acceptable pre-rinse using 150 grams of boiling water.

I take not yet accumulated whatever applied evidence for this, simply I suspect that using unbleached filters might both reduce channeling in all situations (because flow is more uniform across the filter surface) and make your brew more robust against clogging (because of the smaller number of large pores), all while having a slightly faster flow rate (because there are more than pores per unit surface) !

The same conclusions hold for chemex, although their much larger filters nigh certainly crave more water during pre-rinse. I haven't washed this experiment, but based on their weight differences (5.four g for Chemex and 1.4 g for Hario), I would recommend using almost 4 times more than rinse h2o.

Another outcome that surprised me was how the Hario tabless filters seem to be worse than the Hario tabbed filters on all metrics; they flow more slowly, have less compatible pores and are more susceptible to clogging compared to the tabbed filters.

The Cafec filters testify all signs of being a weird case of filters that are bleached more than gently; both their pore distribution quality and ability to taint water is in betwixt the bleached and unbleached cases. If you are really agape of paper sense of taste or hate using a lot of water to pre-rinse your filter, they might be the optimal solution for you, but keep in mind that they flow much slower than other newspaper filters.

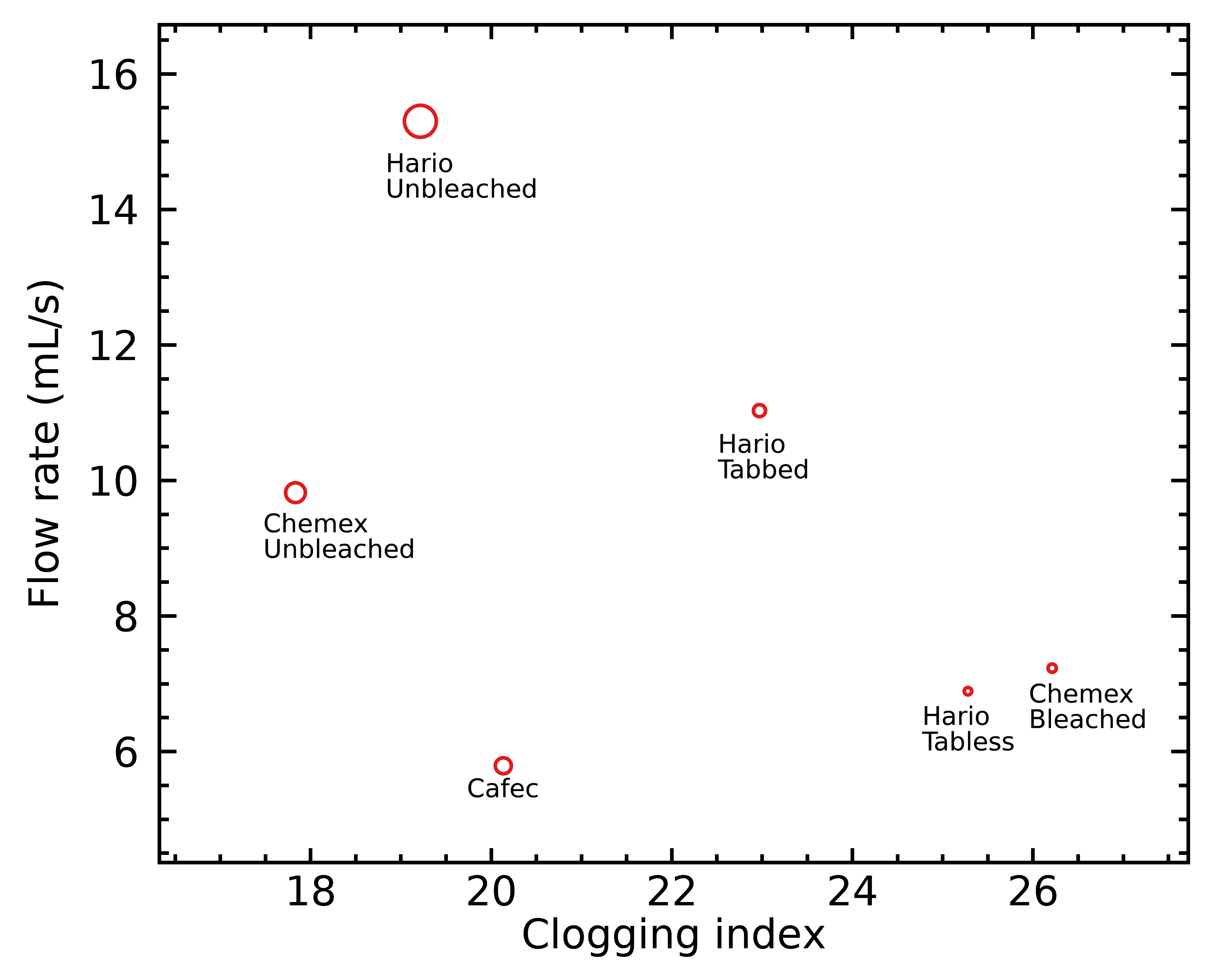
All of these conclusions tin can be visualized in the figure beneath, where I placed all paper pour over filters on a graph of clogging index versus catamenia rate; filters further toward the right are more easy to clog, and those toward the meridian flow faster. I also used larger symbols for the filters that take a more compatible flow across the filter surface, which ways that larger symbols should be less susceptible to channeling regardless of your brew technique.

Aeropress Filters

For Aeropress, we actually only accept 2 contenders here, as I doubt people will start ordering and cutting Whatman filters for their Aeropress brews. But even if yous had the motivation to do so, it seems that the Aesir filters come out at the top in terms of their robustness confronting both channeling and clogging. They do seem to period slower however, because they are almost twice every bit thick compared to the standard Aeropress filters; they accept more pores per expanse than Aeropress, but probably not enough to make upward for their thickness. However, call up that an Aeropress brews take another variable that is not attainable to pour over; you lot tin can press harder, and make up for that difference.

It seems to me that Aesir filters are therefore more desirable for Aeropress brews, which did friction match my very limited and subjective experience.

What does a Clogged Filter Look Like ?

I decided to too try something fun with the microscope, and imaged a clogged and dried V60 Hario tabless newspaper filter:

We can conspicuously see that pores are stained with a brown color, perhaps caused by coffee oil, but nosotros cannot see obvious fines blocking the archway of a pore. That isn't too surprising, as we might await clogging to happen a little deeper than the filter surface.

I promise yous enjoyed this post ! It is definitely the ane that required by far the largest amount of work withal, only I think information technology was worth it.

Acknowledgements

I'd like to requite a special thanks to Alex Levitt for sending me Cafec filters, and Scott Rao for giving me Chemex bleached filters, and for useful discussions without which I would non have thought about the possible importance of the uniformity index. I would also similar to give thanks Doug Weber for useful comments.